F# has many features which can lead to expressing complex domains in a terse and typesafe way. To show this we can codify the world of Dogshorts, the private school for young witches and wizards.
Dogshorts has different houses where students live during their stay. They can belong to either the Gryffin, Snake, Badger or Raven house. We can use a discriminated union to represent these states.
Discriminated unions are also known as ‘sum types’, they are a way of combining sets of types. As an example, consider the labelling of hotel rooms. We label some hotel rooms by their number and some by a name, such as the ‘Royal suite’. HotelRoom models this concept, it can either be a Number of type int or a Nameof type string.
type HotelRoom = Number of int | Name of string
// both are type HotelRoom
let room1 = Number 1
let royalSuite = Name "Royal suite"
We can define the Dogshorts houses as a union of the four house names. This simple use of a discriminated union is similar in concept to an enum.
type House = Gryffin | Snake | Badger | Raven
House sorting
Students are sorted into the appropriate House based on their Wit, Bravery, Cunning and Loyalty.
These traits are properties of type int in a Traits record, which is like a labelled, immutable tuple.
Before the sorting ceremony the student can be modelled as an Unsorted record:
type Traits = {
Wit: int
Bravery: int
Cunning: int
Loyalty: int
}
type Unsorted = {
Name: string
Age: int
Cash: Cash
Traits: Traits
}
The sorting is a function which takes in an Unsorted student and returns a House:
let sorting student =
match student.Traits with
| x when x.Loyalty > 7 -> Badger
| x when x.Bravery > 7 -> Gryffin
| x when x.Cunning > 7 -> Snake
| x when x.Wit > 7 -> Raven
| _ -> Badger
The function uses pattern matching on the student’s Traits and returns the most appropriate house. Students with traits over 7 in Loyalty, Bravery, Cunning, Wit belong in the Badger, Gryffin, Snake and Raven houses respectively. The rest of the students belong to the Badger house.
School fees
To be sorted the student needs to pay school fees and has an amount of Cash to pay these fees.
The monetary system of the magical world consists of three main coins: bronze knuts, silver sickles and gold galleons. There are 29 knuts to a sickle and 17 sickles to a galleon. The wizarding economic system is a simple one with the smallest divisible part being a knut.
We can model a person’s wealth as integers in a Cash record:
type Cash = {
Knuts: int<bronzeKnut>
Sickles: int<silverSickle>
Galleons: int<goldGalleon>
}
The type definition for Knuts seems to specify an int of generic type bronzeKnut. Similar definitions exist for Sickles (silverSickle) and Galleons (goldenGalleon). These are examples of F#’s units of measure, which are extra type annotations that can be added to numeric types.
We can define the relationships between the units of measure to model the wizarding currency:
[<Measure>] type bronzeKnut
[<Measure>] type silverSickle
[<Measure>] type goldGalleon
let knutsPerSickle = 29<bronzeKnut/silverSickle>
let sicklesPerGalleon = 17<silverSickle/goldGalleon>
The knutsPerSickle and sicklesPerGalleon are conversion factors. These are useful to project the type information when performing operations on values. If one tries to add a value of type int<bronzeKnuts> with int<silverSickle>, or divide a value of type int<silverSickle> by knutsPerSickle and pass the value into a functions which expects int<silverSickle>, then the project will not compile.
We can define a function to be able to compare monetary amounts:
let cashAsKnuts cash =
let sickles = (cash.Galleons * sicklesPerGalleon) + cash.Sickles
(sickles * knutsPerSickle) + cash.Knuts
School registration
We can define a type for a registered Student and the schoolFee as 10 bronze knuts:
type Student = {
Name: string
Age: int
Cash: Cash
House: House
}
let schoolFee = 10<bronzeKnut>
Students who can afford the fee can register. In our model this is the transformation Unsorted -> Student. We can define a registerStudent function which takes in an Unsorted and returns a Student option. This returns Some Student if a student can afford the fee and None if not.
let registerStudent (unsorted: Unsorted) =
let isAbleToPay = cashAsKnuts unsorted.Cash > schoolFee
if not isAbleToPay then
None
else
Some {
Name = unsorted.Name
Age = unsorted.Age
House = sorting unsorted
Cash = { unsorted.Cash with
Knuts = unsorted.Cash.Knuts - schoolFee
}
}
The registered Student contains the Name and Age of the Unsorted record. The Cash record is copied with the Knuts minus the schoolFee.
Playing in the grounds
Once a student is registered they become an inhabitant of Dogshorts academy. Other types of inhabitants include Teachers and Ghosts:
type Teacher = {
Name: string
Age: int
Cash: Cash
}
type Ghost = {
Name: string
House: House option
}
Teachers are contractually obliged to have no preference for any of the houses, but have the mortal restraint of Age and the need for Cash. Ghosts can stay loyal to their former house, if they had one.
We can use a discriminated union to codify a type to express the possible inhabitants of the school:
type DogshortsInhabitant =
| Teacher of Teacher
| Student of Student
| Ghost of Ghost
A DogshortsInhabitant can either be a Teacher, Student or Ghost. With the inhabitants defined we can codify some of the school rules.
The school grounds contain magnificent but dangerous woods, which are out of bounds to some of the inhabitants. Teachers can patrol the woods and no one would attempt to restrain the ghosts’ passage. Students are not allowed to enter the area until their 16th birthday.
We can codify this rule as a function:
let canEnterTheWoods inhabitant =
match inhabitant with
| Teacher _ -> true
| Ghost _ -> true
| Student s -> s.Age > 15
Teacher and Ghost return true as they are permitted to enter the woods. Student matches to the variable s and returns true if the student’s Age is over 15.
canEnterTheWoods takes in a single parameter inhabitant and returns a bool with the types inferred by the compiler.
The compiler searches for discriminated unions with the matched Identifiers. DogshortsInhabitant matches to Teacher or Student or Ghost, so this is the correct type.
Lamenters arrive
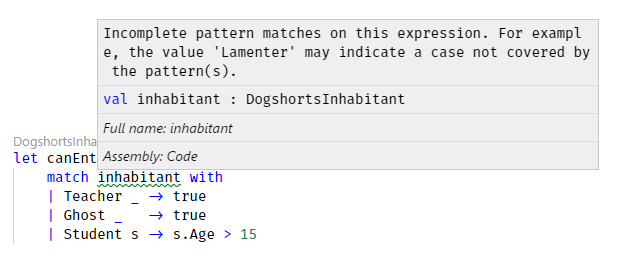
Halfway through the school year we see the return of the Lamenters. Lamenters are a curious bunch who possess no name and no age, they are pure beings of supernatural complaining talents. Their arrival requires an update to our definition of DogshortsInhabitant:
type DogshortsInhabitant =
| Teacher of Teacher
| Student of Student
| Ghost of Ghost
| Lamenter
The addition of an identifier in the DogshortsInhabitant type has an interesting effect. The match expression in canEnterTheWoods is now missing a case and produces a compiler warning to add a case for the value Lamenter.
Conclusion
F# has many language features which can declare a domain in a terse and typesafe way.
Record classes define data structures with minimal boilerplate code. They are immutable which makes it easier to reason about a programs state.
Units of Measure provide a layer of typing on numerics which can eliminate certain kinds of bugs. Other languages can achieve this type safety by wrapping the numeric type. This approach comes with lots of boilerplate code and potential performance overheads.
Discriminated Unions are a powerful tool for mapping intuitive types to a domain. They can also help code correctness by making illegal program states unrepresentable.
Pattern matching on these types can allow detection of the effects of domain changes. An example of this is the addition of Lamenter to DogshortsInhabitant resulted in a compiler warning.
This post is a shallow look at the concepts presented. For a more in depth view I recommend the website F# for fun and profit and the authors’ brilliant talk on Domain modelling.

