In my previous blog posts on the Game of Life I explored how functional programming techniques can result in clear and concise code. However, the benefits of functional programming are more than just cosmetic. You’ve probably heard that functions and the use of constants make it easier to write applications that make use of concurrency. In this post I put this theory into practice!
This post shows how the simple task of computing a Mandelbrot set can be split up across multiple threads (and processors) as follows:
generateDatapoints().concurrentMap({
// a closure that is executed concurrently for each datapoint
(location: ComplexNumber) in
self.computeTterationsForLocation(location)
}, {
// when the above computation completes, send the data to the UI
mandelbrotView.render($0)
})I’ll also explore various optimisations techniques including lock-free concurrency.
The Mandelbrot Set
The Mandelbrot set is described by a stunningly simple mathematical equation; it is the set of complex numbers c for which the following equation does not tend to infinity:
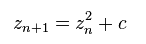
It is possible to implement this equation with just a few lines of code. However, despite its simplicity the Mandelbrot set exhibits tremendous complexity and beauty.
While studying this equation Benoit Mandelbrot coined the term ‘fractal’ as a description of the complex and repeating shapes revealed at the boundaries of the set.
Clouds are not spheres, mountains are not cones, coastlines are not circles, and bark is not smooth, nor does lightning travel in a straight line. - Benoit Mandelbrot
I can still remember many years ago using the freeware Fracint software to render fractals, pixel by pixel, on a 386 computer!
Anyhow, back to Swift …
Complex Numbers
If you hunt around the internet for an implementation of the Mandelbrot set, you will typically come across something like this:
let CONSTANTS = (
iterations: 10_000,
escape: 2.0
)
func iterationsForLocation(cx: Double, cy: Double) -> Int? {
let bounds = CONSTANTS.escape * CONSTANTS.escape
var iteration = 0
var zx = 0.0
var zy = 0.0
while (zx * zx + zy * zy < bounds && iteration < CONSTANTS.iterations) {
let tmp = zx * zx - zy * zy + cx
zy = 2.0 * zx * zy + cy
zx = tmp
iteration++
}
return iteration < CONSTANTS.iterations ? iteration : nil
}The above code takes a point c, described by its real and imaginary components, and determines how many iterations are required to ‘escape’ a given boundary.
Considering the simplicity of the equation that describes the Mandelbrot set, the above code is rather complicated looking!
The code can be improved significantly by introducing a complex number type, which is implemented as a struct:
struct ComplexNumber
{
let real = 0.0
let imaginary = 0.0
func normal() -> Double {
return real * real + imaginary * imaginary
}
}
func + (x: ComplexNumber, y: ComplexNumber) -> ComplexNumber {
return ComplexNumber(real: x.real + y.real,
imaginary: x.imaginary + y.imaginary)
}
func * (x: ComplexNumber, y: ComplexNumber) -> ComplexNumber {
return ComplexNumber(real: x.real * y.real - x.imaginary * y.imaginary,
imaginary: x.real * y.imaginary + x.imaginary * y.real)
}Using the ComplexNumber type the number of iterations for a given location can be computed as follows:
class func iterationsForLocation(c: ComplexNumber) -> Int? {
var iteration = 0
var z = ComplexNumber()
do {
z = z * z + c
iteration++
} while (z.normal() < CONSTANTS.escape && iteration < CONSTANTS.iterations)
return iteration < CONSTANTS.iterations ? iteration : nil
}This is a much more succinct implementation where the Mandelbrot equation, z = z * z + c, is clearly visible.
A Functional Mandelbrot
The ‘standard’ approach to rendering the Mandelbrot is to employ a couple of nested for-loops, one for x (imaginary) and one for y (real), computing the iterations at each location. However, this is not a terribly functional approach! Let’s look at a different approach …
The following code expands the constants tuple to add the X & Y scale:
struct Scale {
let start: Double
let end: Double
let step: Double
func toStride() -> StrideThrough<Double> {
return stride(from: start, through: end, by: step)
}
func steps() -> Int {
return Int(floor((end - start) / step))
}
}
let CONSTANTS = (
xscale: Scale(start: -0.67, end: -0.45, step: 0.0008),
yscale: Scale(start: -0.67, end: -0.34, step: 0.0006),
iterations: 10_000,
escape: 2.0
)I’ve found this to be quite a good use of tuples with named properties, as containers for constant values.
The constants and Scale type can be used to generate an array of datapoints, one for each pixel in the Mandelbrot set that is being generated:
class func generateDatapoints() -> [ComplexNumber] {
var datapoints = [ComplexNumber](count: CONSTANTS.xscale.steps() * CONSTANTS.yscale.steps(),
repeatedValue: ComplexNumber())
var index = 0
for dx in CONSTANTS.xscale.toStride() {
for dy in CONSTANTS.yscale.toStride() {
datapoints[index] = ComplexNumber(real: dy, imaginary: dx)
index++
}
}
return datapoints
}Notice that the above function creates an array that can contain the full 151,250 items (based on the constant definitions above) and updates via index, rather than starting with a zero-length array and appending each item. This is approximately x4 faster in this instance (measuring using Release build -Os).
Once the datapoints have been generated, Mandelbrot construction becomes a simple map operation:
typealias MandelbrotPoint = (ComplexNumber, Int?)
class func functionalMandelbrot() -> [MandelbrotPoint] {
return generateDatapoints()
.map { ($0, self.iterationsForLocation($0)) }
}Each datapoint, which is a ComplexNumber, is mapped to a tuple of type MandelbrotPoint which pairs the complex number with the number of iterations.
With some suitable rendering code in place, this creates a pretty Mandelbrot image:

NOTE: For fast pixel-based image rendering, ignore my Core Graphics code! Instead, I’d recommend looking at Joseph Lord’s post “Drawing Images From Pixel Data - In Swift”, his approach is much faster ;-)
The above code is functional, but isn’t exactly efficient in that it doesn’t use all of the resources at our disposal. While the Mandelbrot number-crunching is underway, the CPU Report reveals the following:
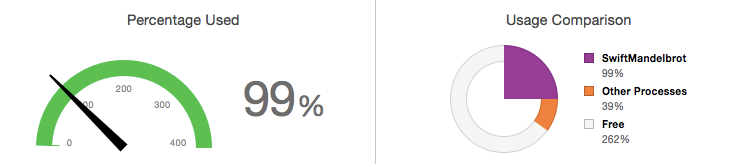
Only 99% of a possible 400% CPU utilisation.
Because the algorithm is running on single thread, it can only be executed on a single CPU. In order to allow utilisation of multiple CPUs, the algorithm needs to be executed concurrently on multiple threads.
Parallel Functional Mandelbrot
A significant advantage of the functional approach to computing the Mandelbrot set, versus the nested for-in alternative, is that it is composed of discrete and independent pieces of work. As a result, we can take these pieces of work and execute them concurrently on different threads, collecting the results together again once they are all completed.
The following code creates a variant of the map operation, which uses dispatch groups to execute the mapping transform concurrently:
func synchronized(sync: AnyObject, fn: ()->()) {
objc_sync_enter(sync)
fn()
objc_sync_exit(sync)
}
extension Array {
func concurrentMap<U>(transform: (T) -> U,
callback: (SequenceOf<U>) -> ()) {
let queue = dispatch_get_global_queue(DISPATCH_QUEUE_PRIORITY_DEFAULT, 0)
let group = dispatch_group_create()
let sync = NSObject()
var index = 0;
// populate the array
let r = transform(self[0] as T)
var results = Array<U>(count: self.count, repeatedValue:r)
for (index, item) in enumerate(self[1..<self.count-1]) {
dispatch_group_async(group, queue) {
let r = transform(item as T)
synchronized(sync) {
results[index] = r
}
}
}
dispatch_group_notify(group, queue) {
callback(SequenceOf(results))
}
}
}The above code iterates over the source array, using dispatch_group_async to execute the given closure expression. This closure performs the transform, then adds the result to the results array. Notice that Swift arrays are not thread safe, so synchronization is used to ensure that only a single thread writes to the array at any one time.
The closure passed to dispatch_group_notify is invoked when all the elements are transformed and the supplied callback is invoked.
The single-threaded map can be replaced with the concurrent version as follows:
generateDatapoints().concurrentMap({
(location, self.computeTterationsForLocation(location))
}, {
// when the above computation completes, send the data to the UI
mandelbrotView.render($0)
})This has the desired effect of using all of the available CPU power:
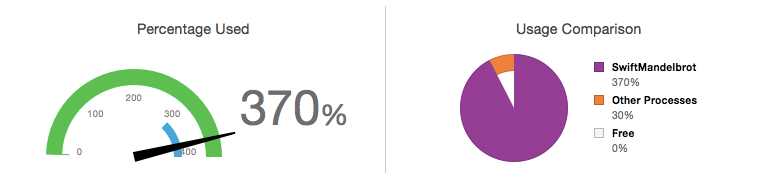
However, there’s a problem. Rendering a typical Mandelbrot, with a maximum iteration count of 1,000, using the original functional algorithm completed in 1.4 seconds, however, the concurrent form executes in 3.8 seconds!
The issue here is that the individual units of work, i.e. the computation of the number of Mandelbrot iterations for a single complex number, are relatively small and fast. In this case, the overhead of the concurrent map function itself is significant in comparison to the underlying work being performed.
There are a few things that can be done to improve performance …
Lock-free Array Updates
One significant issue with the concurrent map operation above is the need to synchronize around the code that updates the results array. As a result, much of the time threads are forced to wait their turn in order to update the results.
Swift arrays have a useful method, withUnsafeMutableBufferPointer, which ensure their contents are arranged in contiguous storage allowing for concurrent updates (thanks to Joseph Lord for this tip!).
Using this approach, the concurrent map can be modified to be free from locking code:
func concurrent<U>(transform: (T) -> U,
callback: (SequenceOf<U>) -> ()) {
let queue = dispatch_get_global_queue(DISPATCH_QUEUE_PRIORITY_DEFAULT, 0)
let group = dispatch_group_create()
// populate the array
let r = transform(self[0] as T)
var results = Array<U>(count: self.count, repeatedValue:r)
results.withUnsafeMutableBufferPointer {
(inout buffer: UnsafeMutableBufferPointer<U>) -> () in
for (index, item) in enumerate(self[1..<self.count-1]) {
dispatch_group_async(group, queue) {
buffer[index] = transform(item)
}
}
dispatch_group_notify(group, queue) {
callback(SequenceOf(buffer))
}
}
}This improves the performance by around 25%.
Batched Computation
Another problem with the current implementation is the overhead of the underlying threading code via dispatch_group_async. The rendering of a typical Mandelbrot might involve computing the iterations for ~200,000 pixels. This requires dispatching 200,000 units of work, and if each unit is small, the overhead is significant.
The final improvement to the concurrent map function is to allow batching of work in ‘chunks’:
func concurrentMap<U>(chunks: Int, transform: (T) -> U,
callback: (SequenceOf<U>) -> ()) {
let queue = dispatch_get_global_queue(DISPATCH_QUEUE_PRIORITY_DEFAULT, 0)
let group = dispatch_group_create()
// populate the array
let r = transform(self[0] as T)
var results = Array<U>(count: self.count, repeatedValue:r)
results.withUnsafeMutableBufferPointer {
(inout buffer: UnsafeMutableBufferPointer<U>) -> () in
for startIndex in stride(from: 1, through: self.count, by: chunks) {
dispatch_group_async(group, queue) {
let endIndex = min(startIndex + chunks, self.count)
let chunkedRange = self[startIndex..<endIndex]
for (index, item) in enumerate(chunkedRange) {
buffer[index + startIndex] = transform(item)
}
}
}
dispatch_group_notify(group, queue) {
callback(SequenceOf(buffer))
}
}
}The above function transforms the source array in batches, minimising the number of dispatch groups that are created.
The batch size is included when invoking the concurrent map:
generateDatapoints().concurrentMap(1_000, {
(location, self.computeTterationsForLocation(location))
}, {
mandelbrotView.render($0)
})This significantly improves performance for small units of work.
Results
The following chart compares the performance of the single-threaded serial implementation versus the various implementations of concurrent map:
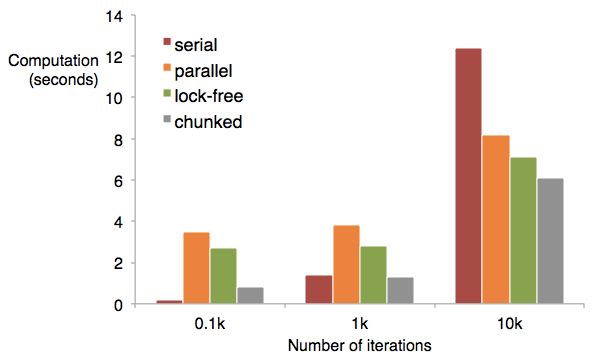
As you can see, for very small numbers of iterations the non-concurrent implementation is faster than any of the parallel versions. However as the Mandelbrot iteration count increases, the various parallel implementations prove to be significantly faster.
You can find the source code for this example application on GitHub.
Regards, Colin E.
