Among the plethora of financial charting applications on the market, if you take a read through their functionality list, you’ll find one of the most common indicators implemented is the Relative Strength Index (RSI). I suppose a good place to start is to give some background on RSI, but if you are a seasoned financial veteran you may want to skip over the next few sections to the good stuff.

So, what is Relative Strength (RS)?

…and why is it important?

Investopedia defines RS with the paragraph: > Relative Strength is a measure of the price trend of a stock or other financial instrument compared to another stock, instrument or industry. It is calculated by taking the price of one asset and dividing it by another.

This has obvious meaning when it is used to compare two instruments (stocks, commodities, currency pairs etc.), but what about when we are only talking about one instrument? Well the norm is to compare the size of instrument gains with the size of instrument losses.

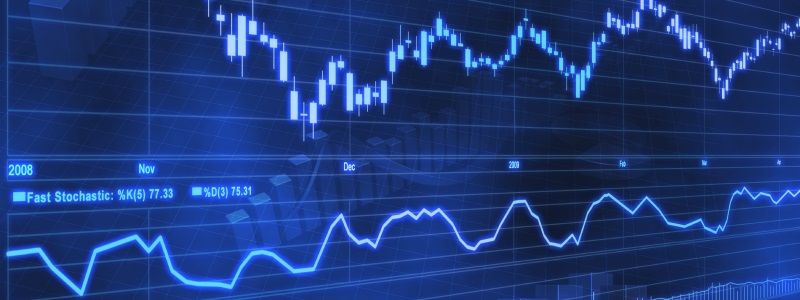
Working it all out

The normal approach to this, is to take a sample of data for a number of defined periods and calculate the total gains over the last 14 days (it’s normal to use 14 periods, which is the default suggested by Wilder in his 1978 book). It is worth mentioning that this is not the net gain but the sum of the gains on each day. Likewise for the losses. From this we have two figures which represent the total gains and the total losses for the specified sample.

If we divide each of these figures by the number of samples then we get the resultant average daily gain and loss. Once we have these figures, we can divide them by each other (normally gains over losses, but not always) to get a “Relative Strength”.

RSI is normally expressed as a value between 0 and 100, so we normalise the figure to a value between 0 and 100 and hey presto, we have our RSI. This allows instruments of various values and volumes to be compared in terms of gain or loss.

RSI is defined as:

RSI = 100 - 100/(1 + RS*)

*Where RS = Average of N days’ up closes / Average of N days’ down closes.

What does it look like?

The image above shows how an RSI is normally represented. The indicator consists of the RSI data series and three horizontal markers showing the mid-point (50 or 0.5), the upper marker or over-buy level (normally 70 or 0.7) and the lower marker or over-sell level (normally 30 or 0.3).

Under normal market conditions you’d expect the data series to hover about the centre line by small deviations. Traders use this level to determine whether or not the current price of the instrument is representative of the market or if it’s unusual.

When the RSI moves above 70 (0.7) the market is said to be over bought and this would normally be reflected by an over inflated price. When the RSI moves below 30 (0.3) the market is said to be over sold and the price is unusually low.

The RSI is primarily used to define risk boundaries and assess the state of a particular market.

Using the component

The code below does not create the dataset, so I’ve assumed that an array of data exists. In order for the RSI component to function, the data must be in a structure similar to that created by the sl.utilities.dataGenerator component.

More information about the data generator can be found in the README.md file on Github.

The chart data is an array of objects with the following structure.

var data = [
    {
        date: new Date(2014, 11, 11),   // start Date/Time of the period
        open: 0.0000,                   // Open Price
        close: 0.0000,                  // Close Price
        high: 0.0000,                   // Highest Price
        low: 0.0000,                    // Lowest Price
        volume: 0                       // Volume Traded
    }
];

Using the component we can simply create an RSI indicator using the code below:

// Create RSI
var rsi = sl.indicators.rsi()
    .xScale(dateScale)
    .yScale(percentageScale)
    .lambda(0.94)
    .upperMarker(70)
    .lowerMarker(30)
    .samplePeriods(14);

indicators.plotArea.append('g')
    .datum(data)
    .call(rsi);

And that’s it, discounting the chart setup code, an RSI indicator in a few lines of code.

The above code does not create the candle chart or any other data series but you can see a full example of this in the examples folder of the project.

Component code walkthrough

While I’ve included relevant code snippets in this blog post, you might want to grab the full project from GitHub.

The component is encapsulated in a namespace as making all of the components global would get messy further down the line. The components all live under the sl namespace and this particular component lives in the sl.indicators namespace. The encapsulation code is shown below.

(function (d3, sl) {
    'use strict';
    sl.indicators.rsi = function () {
        // ... Component code in here ... 
        return rsi;
    };
}(d3, sl));

The first thing we do is define our members, the most important of these being the rsi() function.

var xScale = d3.time.scale(),
    yScale = d3.scale.linear(),
    samplePeriods = 0,
    upperMarker = 70,
    lowerMarker = 30,
    lambda = 1.0,
    css = '';
var upper = null,
    centre = null,
    lower = null;
var rsi = function (selection) {
    // ... Component code in here ... 
};

These variables are private, but the first block are exposed by a set of property setting/getting functions at the bottom of the code file. I’ve not included them in this blog as property setting/getting is a pretty well covered Javascript topic. The second block, namely upper, centre and lower are variables to store handles to the horizontal line elements.

The rsi function

The rsi() function is passed a D3 selection as it’s only parameter. The first thing we do is create the upper, centre and lower markers and this is a one off thing. These markers will be fixed for as long as the indicator persists on the chart. The code block below shows this creation. Each marker is passed a common class name and a specific class name so the style of the markers can be changed in the document CSS.

upper = selection.append('line')
    .attr('class', 'marker upper')
    .attr('x1', xScale.range()[0]) 
    .attr('y1', yScale(70))
    .attr('x2', xScale.range()[1]) 
    .attr('y2', yScale(70));
centre = selection.append('line')
    .attr('class', 'marker centre')
    .attr('x1', xScale.range()[0]) 
    .attr('y1', yScale(50))
    .attr('x2', xScale.range()[1]) 
    .attr('y2', yScale(50));
lower = selection.append('line')
    .attr('class', 'marker lower')
    .attr('x1', xScale.range()[0]) 
    .attr('y1', yScale(30))
    .attr('x2', xScale.range()[1]) 
    .attr('y2', yScale(30));

The next thing to do is to create the line which will represent the RSI data series. The line creation is shown in the code block below. Of course we can link the X position of each point directly to the date field in the data. No calculation is necessary but we need to calculate the Y position after first calculating the RSI.

var line = d3.svg.line();
line.x(function (d) { return xScale(d.date); });
selection.each(function (data) {
    if (samplePeriods === 0) {
        line.y(function (d) { return yScale(0); });
    }
    else {
        line.y(function (d, i) {
            // ... Calculate the Y series position here ... 
            return yScale(rsi);
        });
    }
});

To calculate the RSI we roll back through the data from the current location and determine whether the data for that period was a gain or a loss. Any gains result in the close price being appended to the up array and 0 to the down array. Any loss is appended to the down array and 0 to the up array. These values are also weighted is lambda is less than 0 to make more recent data points more significant in the moving average.

We continue to do this for each period. We average the array values and use these in our RSI formula.

• First we fill the arrays depending on Gain or Loss

for( var offset = to; offset >= from; offset--) {
    var dnow = data[offset],
        dprev = data[offset-1];
    var weight = Math.pow(lambda, offset);
    up.push(dnow.close > dprev.close ? (dnow.close - dprev.close) * weight : 0);
    down.push(dnow.close < dprev.close ? (dprev.close - dnow.close) * weight : 0);
}

• Note the weight variable to weight the moving average this is an exponential of the lambda property which can be set but is set to 1.0 by default.
• Then we use the arrays to calculate the RSI using the formula at the top of this post

var rsi = (up.length > 0 && down.length > 0 ) ?
    100 - (100/(1+(d3.mean(up)/d3.mean(down)))) :
    0;

Should any value not be valid the rsi() function returns 0. As you can see the line’s Y value has now been set and we can append it to the RSI data series path.

var path = d3.select(this).selectAll('.rsi')
    .data([data]);
path.enter().append('path');
path.attr('d', line)
    .classed('rsi', true)
    .classed(css, true);
path.exit().remove();

I hope this gives a detailed overview of the RSI component and some insight in to the uses of RSI.

The complete code

All of the components are available on GitHub with the RSI component being located in the /components/indicators/ folder.