Cloud computing gives software applications the ability to scale up on demand. With sufficient financial resources, enough compute power can be thrown at a (well-written) software application to achieve desirable performance goals. Why then have cloud providers introduced High Performance Computing components (think hardware accelerators, fast network adapters, etc.) into their clouds? If you can already scale vertically (to a large extent) with high-level programming languages, why would you add the complexity of hardware-level programming into the mix?!
What is High Performance Computing?
High Performance Computing or HPC is not for every application. HPC applications are usually highly numeric (involving lots of mathematical calculations) and have large datasets (data cannot fit on one computer), which means that they can take a long time on traditional hardware. Most applications involve simulations (or modelling) and more recently Data Analytics or Machine Learning. Some applications like Financial Trading are more focussed on reducing latency than necessarily dealing with large datasets or calculations.
To really appreciate what HPC can do, let’s revisit what is involved in performing computations. Figure 1 below shows a block diagram of the main building blocks within a computer (left) and a network of computers (right). In a typical computation, data is taken from some storage element, transported to a compute element, where an operation is performed on it and the result is transported back to storage. While it is also possible for data to originate from an external source (like a database or web server, often over a network), the main concern is that it takes time to transfer data from a source, perform the computation and send the results to its storage destination.
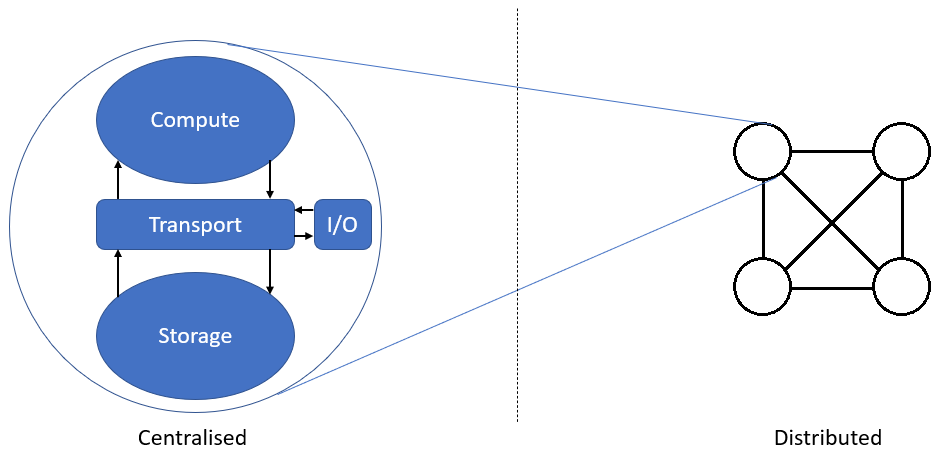 Figure 1: Computation Building Blocks
Figure 1: Computation Building Blocks
The main performance goal in computing systems is centred around reducing the round-trip time for computations. This is typically done by reducing the number of overall trips made for the high-level calculation and/or reducing the time it takes to complete one or more stages of a calculation. In modern computers, like the one shown in Figure 2 below, a memory hierarchy is employed to reduce the time to transfer data to and from “storage”.
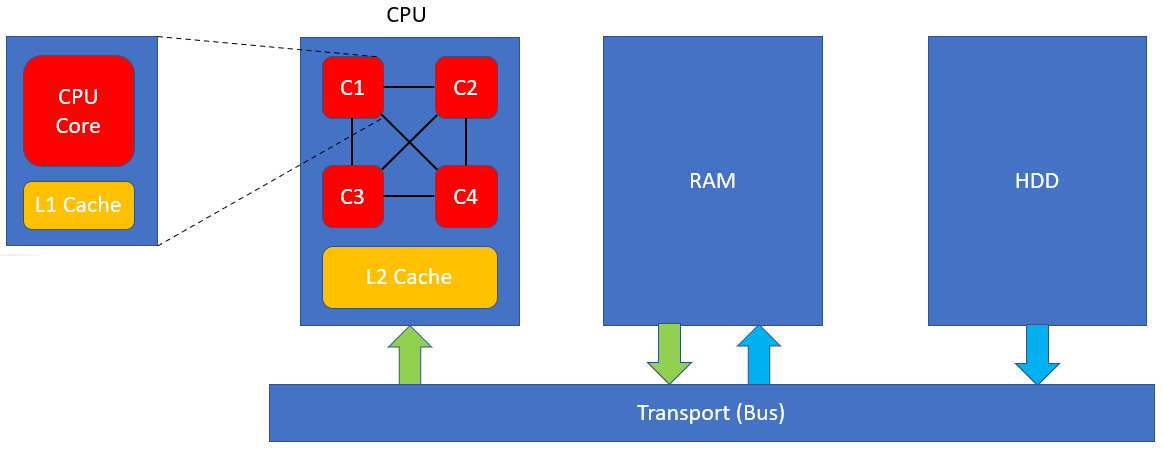 Figure 2: Modern Computer
Figure 2: Modern Computer
On computer start-up, data starts off in the Hard Drive (HDD) and is transferred to the smaller but faster RAM (see blue arrows in Figure 2) before the CPU interacts with it. Data can then transferred between the RAM and CPU (green arrows in Figure 2), allowing for faster access than from the Hard Drive directly. To further reduce transfer times, modern CPUs utilise multiple levels of memory caches to temporarily store data. The challenge for programmers is to try to keep as much data in these caches for as long as possible when writing performant programs.
Utilising low-latency memories can also improve data transfer times. At the cluster level, transfer times can be minimised by utlising fast networking technologies, such as Infiniband, and the right network topologies for your application. For example, stencil applications such as lattice QCD benefit from a Torus topology (see Figure 3).
 Figure 3: Supercomputer Network Topologies (hpcwire.com)
Figure 3: Supercomputer Network Topologies (hpcwire.com)
Apart from reducing the time for the data transfer phases of computation, the computational efficiency of compute elements can also be improved by performing as many operations as possible in parallel. CPU cores traditionally have one Arithmetic Logic Unit (ALU) that performs operations on at most 2 data words, i.e. x-bit numbers (where x = 32,64, etc), at a time. While modern cores also contain vector units (multiple ALUs), these offer limited parallelism (usually 4 or 8 parallel operations). Figure 4 below shows how various hardware accelerators can be used as co-processors within a computer system to perform multiple computations in parallel. GPUs utilise many (100s of) vector units to perform the same operation on multiple data words in parallel. Accelerators like FPGAs, ASICs and TPUs utilise replicated data pipelines of application-specific logic to operate on multiple data words simultaneously.
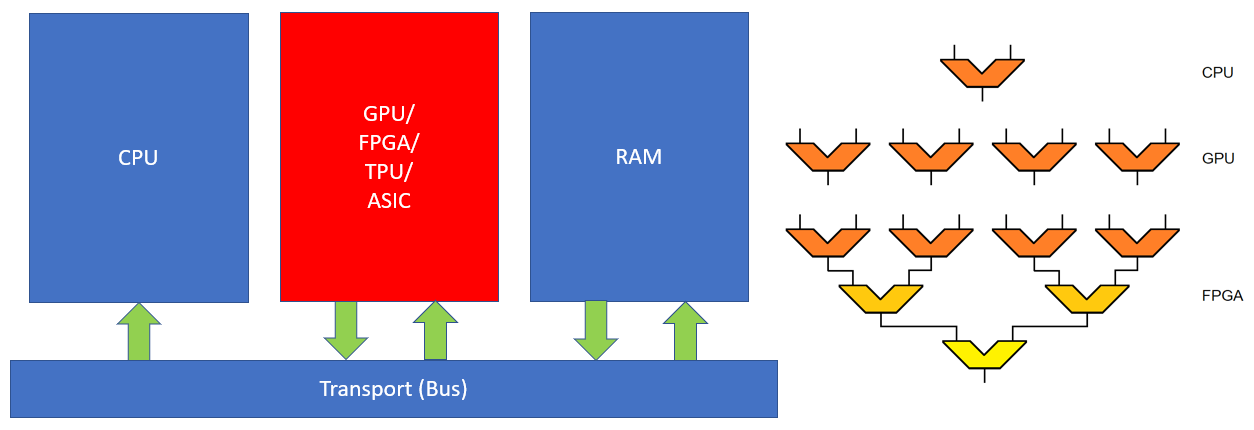 Figure 4: Hardware Accelerators
Figure 4: Hardware Accelerators
HPC in the Cloud
Now that we see how HPC can be used to improve data transfer speeds and computational efficiency, let’s look at when to use HPC in the Cloud. The most important step in knowing where to apply HPC is understanding where it will be most beneficial. To this end, it is important to understand the performance limiting factor(s) in a given application. Table 1 below highlights how HPC devices can be used to tackle various application performance problems.
| Performance Limitation | HPC Solution |
|---|---|
| Compute-bound | Improve computational efficiency (hardware accelerator suited to application characteristics) |
| Memory-bound | Improve interconnect speeds between processors and memory on same machine (low-latency memory) |
| I/O-bound | Improve interconnect speeds between computer nodes (low-latency network adapters) |
Table 1: HPC solutions to application performance problems
Once the performance bottlenecks have been identified (through analysis and profiling), it is important to consider the impact of using these technologies on the code (see Table 2 below). Important considerations around this include whether appropriate talent (programmers with the right skill-set) and tooling (libraries, frameworks, documentation, tutorials, etc) is available to utilise these technologies effectively.
| HPC Device | Impact on code |
|---|---|
| Hardware Accelerator | Make use of high-level or low-level libraries or programming languages |
| Fast Memory | Transparent to the programmer |
| Fast Network Adapters | Make use of libraries or can be transparent to programmer |
Table 2: Impact of incorporating HPC solutions on programming
Apart from considering the use of HPC devices, it is equally important to consider the operational side of running your application in the Cloud, which can also include application code/design changes. If starting from code that is both non-HPC and not Cloud-ready, it is important to consider both aspects holistically since there can be overlapping concerns, especially in application inter-node communication. It may also be worthwhile to perform such a migration in phases, e.g. non-Cloud to Cloud-ready, before utilising HPC. In general, it is important to be aware of additional scaling considerations for HPC clusters such as comparing the cost of running one HPC node versus an equally performing set of regular nodes.
Conclusion
With the performance benefits from Cloud-scaling reaching to a point of diminishing returns for some large-scale applications, Cloud computing has had to add new tools to its artillery to keep up with demand (similar to the use of multi-cores at the end of Dennard-scaling). While very few organisations are capable of running applications that require this level of scale, interest in using HPC in the Cloud continues to grow. Cloud providers are also innovating in this space, utilising existing HPC resources to provide managed services such as Data Transfer, Data Analytics and Content Delivery Networks. The popularity of using HPC components to achieve performance at the edge of the Cloud also seems to be increasing, especially in the machine learning space. It will be very interesting to see how HPC concepts continue to propagate beyond the edge of the Cloud.


